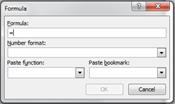
ClariCalc User’s Manual

ClariCalc performs calculations on expressions written in standard math notation. That is a broad statement, so the following section covers some nuances.

Notation

Decimal symbol

Some countries use a dot for their decimal symbol. Others use a comma. ClariCalc can do either. It chooses the symbol per the settings in the Windows control panel. [Warning: comma decimal is only lightly tested.]

Multiplication

Function argument separator

ClariCalc uses the semi-colon, not the comma, to separate function argu­ments, as in:  x = max(a; b; c)

Variable names

Variable names may be multiple characters long. They must begin with a letter from the Latin or Greek alphabet. The rest of the characters may be letters or numerals (0123456789). An under-score within a name is allowed and will be interpreted to mean the start of a subscript. Primes at the end are ok, e.g., f_c′. So are accents, e.g., \(\bar{y}\), \(\hat{\theta}\), etc.

Superscripts

ClariCalc will read a superscript as an exponent.

Special Fractions

Number Names and Bases

z*

ClariCalc will find the complex conjugate of a variable noted z^*

When you run a calculation, ClariCalc will set variables to italic. It will set function names (e.g. sin), units (e.g. meters), and logic words (if and or not xor else otherwise) to non-italic.

Operators

Operator	Keyboard Shortcut	Example	Comment
=		x = 15	Assign a value to a variable. Assignment statements must begin at the start of a paragraph or just after a tab.
+		2 + 2	Addition
–		5 – 3	Subtraction
-		-4	Unary minus
*		2 * 4	Multiplication of numbers. Memberwise product of arrays.
×	\times	2 × 4	Multiplication of numbers. Cross product of vectors.
·	.	a · b	Multiplication of numbers. Dot product of matrices, or vectors.
		(2)(4)	Multiplication
		2 a	Multiplication. [▼]ClariCalc checks each blank space in an expression and inserts a multipli­cation where appropriate.
		2a	Multiplication
		a2	Not a multipli­cation. ClariCalc reads a2 as a variable name.
		a(2)	Either a function a(2) or a multipli­cation a×2. [▼]If a valid function name exists, it will take precedence over multipli­cation in this syntax. Using this syntax for multipli­cation is legal, but i do not recom­mend it. If you type a space between a factor and a following paren, as in a (2), you will make it easier for a reader to tell the difference between a multipli­cation and a function.
/		\(\frac{8}{2}\)	Division
÷	\div	8 ÷ 2	Division
∕	\ldiv	8 ∕ 2	Division with inline format.
^		32	Exponent
√	\sqrt or \r	\(\sqrt{4}\)	Square root
\(\sqrt[n]a\)	\r(n&a)	\(\sqrt[3]{27}\)	nth-root
%		10%	Percent
‰		10‰	Per thousand
|  |		|-4|	Absolute value of a scalar, determinant of a matrix, or magnitude of a vector.
\(\lVert\,\,\,\rVert\)	\Vert	\(\lVert x \rVert\)	\(\sqrt{x_1^2+\cdots +x_n^2}\) if the argument is a vector of reals
			\(\sqrt{|z_1|^2+\cdots +|z_n|^2}\) if the argument is a complex vector
			\(\sqrt{\sum_i\sum_j A_{i;j}^2}\) if the argument is a matrix
⌊ ⌋	\lfloor \rfloor	⌊4.5⌋	Floor. Always rounds down.
⌈ ⌉	\lceil \rceil	⌈4.5⌉	Ceiling. Always rounds up.
!		5!	Factorial
‼	!!	5‼	Double Factorial
¡	0161	5¡	Subfactorial, n¡ = \(\left\lfloor{\frac{n!}{e}+\frac{1}{2}}\right\rfloor \)
\(\binom{n}{k}\)	(n\atop k)	\(\binom{5}{3}\)	Binomial coefficient. \(\binom{n}{k}=\frac{n!}{k!(n-k)!}\)
^*		z*	Complex conjugate
∠	\angle	r∠θ	Polar notation separator
\		a \ b F \ S	Integer division on numbers a and b = ⌊a ÷ b⌋ Matrix direct solution if F and S are matrices and S is square. [▼]Matrices can be used to express a sytem of linear equations, such as S×D = F. One can solve such a system by matrix inversion, D = S⁻¹ × F, but the direct solution, F \ S, has a faster algorithm.
<			Comparison Operators. For If Expressions, such as: x = a if (n < 2) else b
>
≤	<=
≥	>=
==
≠	=/
≅	~=		Comparison operators that return True for magnitudes that are equal ± 0.1%. Useful when dealing with floating point error in engineering calculations.
≲	<~
≳	>~
≉	~/		Returns True for comparisons that are more than 0.1% apart.
and			Logical operators. For If Expressions, such as: x = a if (n < 2 and c == 2) else b not and ¬ are unary operators, as in: x = a if (not n == 2) else b
or
not
xor
¬	\neg
∧	\wedge
∨	\vee
:		2:3	Integer range separator. The term V[2:5] will return an vector containing elements 2 through 5 of vector V. The term table[1].range[4; 2:5] will return an array that contains the contents of table 1, row 4, columns 2 through 5. The comprehension [2 i for i in start:end] will return a vector after it executes the expression “2 i ” several times, with variable i taking on each integer value in the range from start to end.

Functions

Constants

π

ClariCalc uses a value of 3.141592653589793238462643383 for π.

e ^z

ClariCalc will treat e just like any other variable most of the time. But if e is the base of an exponent, for example: e ^x or e ^{(3 a)}, then ClariCalc will perform the function exp(z).

Operator Precedence

If Expressions

ClariCalc has two kinds of if expressions.

Inline If Expression

Cases Expression

Conditions may contain logical operators: and or not xor

x = 2a if (a < b and b == 5) else a²

Chained comparisons are okay.

x = 1.0 if (a < b < 5 < d) else 1.3

In an inline expression, the equals comparison operator must be ==. In a cases expression, you can use either = or ==.

x = 1.0 if (a == 12) else 1.3

Rounding

If you write variables into your equations, ClariCalc will search your document for values to plug in. Here's an example.

Result:

x = \(a+\frac{b}{c}\)a+b/c = \(\color{#3333CC}{7+\frac{11.2}{-4}}\) = 4.2

When an expression contains variables, ClariCalc will:

1. Search for the variable assignments.
     a.   First in bookmarks and ParentFiles.
     b.   Then upwards in the document for variable assignments.
2. Write an echo of the expression, with the values plugged in.
3. Do the calculation and write the result.

To assign a value to a variable, just write

variableName = value at the start of a paragraph, or after a tab.

More examples:

L = 14	← Write assignments at the start of a paragraph.
w = 0.12	P = 2.3	← or after a tab.

M = \(\frac{w\,L^2}{8}+\frac{P\,L}{4}\) = \(\color{#3333CC}{\frac{(0.12)(14^2)}{8}+\frac{(2.3)(14)}{4}}\) = 10.99

A ClariCalc search for a variable goes in the upward direction. So if you have defined d more than once, ClariCalc will find the place that is (1) above the calculation line, and. (2) closest to the calculation line.

A variable search is case-sensitive. A search for E will not find e.

Variable names may be multiple characters. They must start with a letter, not a number. Other characters may be letters or numbers. Subscripts are ok. Primes at the end are ok, e.g., f_c′. So are accents, e.g., \(\bar{y}\), \(\hat{\theta}\), etc.

To assign a text string, put the text inside quotes, e.g., s = a string

Note that ClariCalc writes an echo of the expression that displays the values used for each variable. This echo allows one to check ClariCalc’s work. The echo is typically colored blue to set it apart from other text.

When a value is sourced from a Bookmark, a Parent File, or from LookupTable.txt, then the value is written in green. This gives a checker a better audit trail for the values.

If you want to suppress the echo (often a bad idea), you can write an ellipsis where the echo would normally go.

Example: t = c - a = … = 5

Speed Tip

Bookmarks

In a really long document, ClariCalc can slow down a little if it has to search a long way back to find a variable. To keep things speedy, ClariCalc has an alternate search method. It uses a Microsoft Word feature called bookmarks that you may not have used before. In Word, a bookmark is a place in the document that has a name. Word keeps track of this place and can find it quickly.

When ClariCalc searches for a variable, it will first look in the list of bookmarks. If ClariCalc finds the variable name in the list of bookmarks, it will use the bookmark, even if the variable name is defined again later in the document. That last sentence is an exception to the usual upward search. Bookmarks are trumps. That's why they're fast.

You can set a lot of bookmarks at once with ClariCalc. For example:

Fy = 36 ksi	E = 29000 ksi	G = 12000 ksi
fc′ = 4500 psi	fc″ = 4500 psi²	fyr = 60000 psi

Select the whole block of text and choose the menu command:

Add-Ins | Insert | Miscellaneous | Bookmark(s).

Word only allows alphanumeric characters in bookmark names. That interferes with certain variable names, so the ClariCalc bookmarking utility examines each proposed name and will make a substitution for the last character in four cases:

fc′	→	fcPrime
fc″	→	fcPPrime
\(\bar y \)	→	yBar
\(\hat{\theta}\)	→	θHat

Remote Bookmarks

A ClariCalc expression can call in a value from a bookmark, even if the bookmark is in a different Word document. To do this, first use the doc() function to assign a particular Word document to an object. The bookmarks of that other document can then be called as attributes of the object. Here’s an example:

stds = doc(Section A.docx)	←	assigns a document to an object named stds
A = stds.L × stds.W F = A × stds.p	←	Two equations that call bookmarks.

You can skip the first step, as in the equation below.

p = doc(Section A.docx).p

You can also call table elements from the other document, as in:

n = stds.table[1].cell[2; 3]

File path

Parent Files

If you want to avoid the Object.Attribute notation, you can assign values in a ParentFile. Here's how:

1. Use a text editor, say NotePad, to create a text file. Write your data into the file using a tab-delimited format like this example:

2. Save the text file with UTF-8 encoding. It can now be used as a parent file.
   Or, skip steps 1 and 2; select a range of assignments, then invoke Add-ins | Edit | Edit | Create Text ParenFile.
3. Place the parent file into the same folder as the descendent file(s), or in any folder that contains the descendent file(s).
4. In each of the descendent files, type in the file name of the parent file, then select that file name and bookmark it with the name ParentFile.

Subsequent variable searches in the descendent files will inherit all the variable assignments in the parent file. Like this:

x = 2 G = (2)(12000) = 24000

A ParentFile has precedence over any variable assignment except a bookmark.

Variable Search of Data with a Lookup Key

If you have a big table of tab-delimited data in a separate text file, ClariCalc can search through it for a lookup value. To call for such a search, a document would contain text that looks something like this:

Section = “W8x31”	←	This line sets a lookup key W8x31.
2 d = (2)(8) =: 16	←	The value for d comes from the entry for W8x31 in LookupTable.txt.

The data in LookupTable.txt can be anything you write. It’s format will look something like the structural steel table shown here:

W	wself	A	d	tw	bf	tf
Section	plf	in2	in	in	in	in
W14x74	74	21.80	14.17	0.450	10.070	0.785
W8x31	31	9.13	8.00	0.285	7.995	0.435
W8x28	28	8.25	8.06	0.285	6.535	0.465
W8x24	24	7.08	7.93	0.245	6.495	0.400

In order to search this table, first set a lookup key for say W14x74. In the rest of the document, ClariCalc variable searches will find values for:

w_self, A, d, t_w, b_f, or t_f

There are two ways to set a lookup key:

1. Select from a list of keys in the menu command:
   Add-Ins | Insert | Lookup Key…
2. Write the key into your document, then hit  L. Example:

Type this:	W14x74 L
Result:	Section = W14x74

You can have more than one lookup key active at one time, provided that they are of different types. For instance, one key (say Section = W14x74) might deliver section properties like A and d. (area and depth for the W14x74 section.)

Another key (say SteelGrade = ASTM A36) might then deliver properties, like F_y and F_u, of a steel grade.

The file with the data is named LookupTable.txt. It must be located in C:\Users\userID\AppData\Roaming\Hilbert\

References to values inside a table

An expression located outside a table can refer to value(s) inside a table using any of the following syntaxes:

The indicator term can be either an integer or a string of text, or a variable that returns an integer or string. An integer refers to a table by its position relative to the expression. A string refers to the nearest (upward) table that starts with that string. Examples:

table(-1)	← refers to the previous table
table(0)	← refers to the table containing the expression
table(2)	← refers to the table after the next table
table(“Fv”)	← refers to the nearest table that starts with Fv

The table’s method and property terms are:

[row; col]	←	returns the contents of one cell.
.cell[]	←	returns the contents of one cell.
.range[]	←	returns an array with the contents of several cells.
.find[]	←	returns an array with the contents of cells from rows that match a string.
.match[]	←	returns an array with the contents of cells from rows that match a regular expression pattern.
.interpolate[]	←	returns a value interpolated between cell values.

.find and.match work only on rows, not on columns.

The row and col terms can take several forms:

Examples for row and col:

[3; 2]	← returns the cell contents at row 3, column 2
[end; 4]	← returns the bottom cell in column 4
[2:3; 4]	← returns a 2x1 list
[4;]	← returns an array containing row 4

Dictionaries

A dictionary, like an array, contains data, but a dictionary is indexed by keys, not integers.

array[3]	← Array calls use an integer.
dictionary[k]	← Dictionary calls use a key, which can be a string.

The syntax that one uses to create a dictionary has pairs of a key and a value surrounded by braces.

Note that keys are separated from values by a colon. Each pair is separated from the others by a semi-colon. Keys need not be surrounded by quotation marks.

You can call a dictionary value in two steps, by assigning a dictionary to a variable and then making the call.

Or you can call a dictionary value in one step by defining the dictionary and the index on the same line. The index can of course be a variable.

Dictionary values cannot be changed and they cannot be nested. They can contain a unit.

L = {court: 94 feet; field: 100 yards}

One can add, multiply, etc., with many things besides real numbers. ClariCalc can help you do that. It operates on dates, arrays, matrices, vectors, comprehensions, and complex numbers.

Date Arithmetic

ClariCalc enables date addition and subtraction.

To assign a date to a variable, place a valid date string inside quotation marks. ClariCalc can recognize some dates even without quotation marks, such as today or now.

d₁ = 12 January 2015

Then use the normal addition and subtraction operators to do date arithmetic. Examples:

As you can see, the echo displays dates in the Short Date format chosen in your Windows Control Panel. ClariCalc writes results in Long Date format.

Arrays

A ClariCalc array is a collection of values stored in a one- or two-dimensional grid. They look like these examples:

\(\begin{pmatrix}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{pmatrix}\)    \(\begin{bmatrix}4\\ 5.5\\ 0.9\end{bmatrix}\)   [11   2.4   800]

One can call an individual value from an array with an index, as in: x = M[1] or y = M[1; 3].

Most ClariCalc operators and functions operate on arrays in an element-wise fashion. If you add a scalar to an array, or pass an array to most functions, ClariCalc will do an element-by-element calculation and return an array.

However, mathematicians have several ways to do multiplication on arrays. In ClariCalc, you choose the type of multiplication by your choice of multiplication symbol:

Here are some other array operations:

There are three ways to write an array:

1. If you click on the \(\tiny \begin{bmatrix}1 & 0 \\0 & 1\end{bmatrix}\) button on the Add-Ins menu, ClariCalc will show a dialog box to help you populate a matrix, such as:
   M = \(\begin{pmatrix}10 & 4 \\0.5 & 103\end{pmatrix}\)
2. Between square brackets with spaces to separate elements and semi-colons to separate rows, as in: V = [10  4] or M = [10  4; 0.5  103]
3. Comprehensions, see below.

To append a scalar onto one end of a vector, write the scalar name and the vector name into another array. Such that:

[a  V] will prepend a to the beginning of vector V.

To concatenate two arrays, write the array names as elements in another array. So that:

Comprehensions

Comprehensions provide a concise way to create a column vector, using a syntax similar to set builder notation in mathematics.

Syntax:

Keyboard Shortcuts

Below are some keyboard shortcuts that I have found useful. There are many more at Word Options | Proofing | AutoCorrect Options… | Math AutoCorrect.

Some of these shortcuts will instantly convert to their target. Others take effect only when (1) a ClariCalc calculation is run, or (2) when you type  m after your formula.

Desired	Input	Comment
Math Zone	=	Creates a Word Math Zone
exponent	^exponent	Works for any exponent or subscript. Builds up in a Math Zone, or during calculation, or when you type alt+m after your formula.
subscript	_subscript
√	\r	Radical
\(\sqrt[b]x\)	\r(b&x)
δ	\delta	Works for many Greek letters. Shortened versions, e.g. \d, work for some Greek letters, but not the ones with short English names, like nu or rho.
Δ	\Delta
·	\cdot	Middle dot, as in: N·m
	.
×	\times
÷	\div
∕	\ldiv	Linear div: a ∕ b Works best in a Math Zone.
′	'	Prime Hit ' twice to get a double prime, ″.
″	\pprime	Double prime
°	\degree	Degree
	o
≤	<=
≥	>=
≠	=/
≉	~/
≅	~=
≲	<~
≳	>~
\(\bar y\)	y\bar	Accents work best in a Math Zone.
\(\hat{\theta}\)	θ\hat
\(\dot{z}\)	z\dot
\(\vec F\)	F\vec
∠	\angle	\an also works.
ø	o//	o with stroke
←	<–
→	–>
⇒	=>
✓	\checkmark
†	\dagger
€	\euro
£	\pound
¥	\yen
fc′	fc'	Starts out as f_c^′ Builds up to fc′ during calculation.
fc″	fc"

Quick Parts

Microsoft Word has a feature called Quick Parts which provides a shortcut to insert a section of text or graphics. It works like this:

Type:

test      (type "test" then press the "F3" button.)

Result:

This is a demonstration of Word’s Quick Parts feature.

You can create Quick Parts entries of your own, or use ones that others have created.

ClariCalc takes the Quick Parts idea and adds some math ability.

Type:

t2 

Result:

x = \(\left(\tfrac{15}3\right)(2)+5\) = 15

With ClariCalc, Quick Parts entries aren't just text. They proceed to do some calculation work.

Choose an Quick Parts Entry from a list

You may end up with a lot of Quick Parts entries. I’ve written several for structural engineers. But it can become difficult to remember them all.

ClariCalc can display a list of all the ClariCalc Quick Parts entries, so that you can choose an entry from the list. To get the list, invoke the command:    Add-Ins | Insert | Quick Part…

Tables

A Word table can do a few of the calculations that you might do in Microsoft Excel. Word's spreadsheet abilities are pretty rudimentary compared to Excel, but ClariCalc helps with some enhancements of its own.

In order to do a calculation in a Word table, first select a table cell, then click on the Table Tools | Layout | Formula button. It will bring up a dialog box for your formula.

Write in your formula and hit ok. Formulas can include cell references like "A1".

Microsoft describes the standard capabilities of such formula fields here.

ClariCalc adds several enhancements:

On the Table Tools | Layout ribbon, ClariCalc adds nine buttons:

• Fill Down and Fill Right.
• Copy and Paste, with automatic adjustment of relative cell references.
• Extend series
• Sum Above
• Increase and Decrease number of digits
• Update Table Formulas

Ordinarily in Word, a row insert or row delete will fail to adjust relative cell references. When ClariCalc is installed, the references are adjusted. (If you don't want a cell reference to be adjusted during Copy & Paste or Fill, then write an "$" before the cell reference.)

ClariCalc Variables

Ordinarily in Word, a formula field can only call variables that are cell references or bookmarks. With ClariCalc, if you calculate using  R, then formula fields in a table can call ClariCalc variables. (This is a slow operation, so you won’t want to over use it.)

References to values inside a table

An expression located outside a table can refer to value(s) inside a table using any of the following syntaxes:

The tbl term can be either an integer or a string of text, or a variable that returns an integer or string. An integer refers to a table by its position relative to the expression. A string refers to the nearest table that starts with that string. Examples:

The table’s method and property terms are:

The row and col terms can take several forms:

Examples for row and col:

Sum a Column

Back in grade school, you did sums that looked like this:

	3.20
	2.55
	7.01
	12.76

That format is easy to read, so ClariCalc makes it easy for you to do. Here's an example from a material takeoff:

Beam 1 = (24 plf)(3)(15 ft) =	1080	lbs
Beam 2 = (15.5 plf)(8)(12 ft) =	1488
Connections = 0.15 Σ = (0.15)(2568) =	385
Total = Σ =	2,953	lbs

The trick is to put the Σ character into your formula. After you’ve done that, just  c or  k like any other calculation. ClariCalc will locate the Σ, and in the calculation echo, it will plug in a sum of the preceding lines’ final numbers.

You can also get this effect by placing the insertion point below the numbers that you want to sum, then clicking on the button at:

Add-Ins | Calculate | Σ

When you sum this way, ClariCalc will automatically set tab stops to align the column.

ok / ng

An engineer will often calculate a value, compare it to an allowable value, and record a decision – either ok or ng (no good).

Example:	Fb = 21,400 psi
	fb = \(\frac {M}{S_x}\) = \(\color{#005696}{\frac{17{,}000\text{ lb}\cdot\text{ft}}{24.3\text{ in}^3}}\) = 8,400 psi < Fb, ok

ClariCalc has a field that will make that comparison and refresh the ok/ng decision every time that you redo a calculation.

Step one is to do the calculation, but stop just before writing ok.

f_b = \(\frac M{S_x}\) = \(\color{#005696}{\frac{17{,}000\text{ lb}\cdot\text{ft}}{24.3\text{ in}^3}}\) = 8,400 psi < F_b,

Step two is to invoke one of these two commands:

ClariCalc will insert the field. Then, every time the calculation is refreshed, it will re-check the comparison. If the value flips to a value that violates your chosen comparison, the field will notify you.

f_b = \(\frac{M}{S_x}\) = \(\color{#005696}{\frac{75{,}000\text{ lb}\cdot\text{ft}}{24.3\text{ in}^3}}\) = 37,000 psi > F_b, ng

If you are interested in the internal contents of the field, you can see them by selecting a field and pressing shift F9. It will look something like this:

{ ◊if 37,000 <= 21,400 ok ng }

The two numbers inside the field correspond to the two values in the comparison. The two values will be converted to SI base units if their assigned units do not exactly match.

Troubleshooting

Answers to some common questions:

The ClariCalc installation didn’t work. What’s wrong?

Watch out for:

1. If Internet Explorer would not download the ClariCalc installation file, try another browser. Chrome works.
2. Exit Word before running ClariCalc-Setup.exe.
3. You need to have Administrator rights to install ClariCalc.
4. Examine your user ID. If you have more than one user profile, ClariCalc may have installed to the wrong folder.

Why didn't ClariCalc find my variable?

ClariCalc only searches for variables at the beginning of a line or after a tab.

Why did ClariCalc find the wrong number for my variable?

Why did ClariCalc add an extra character after the "=" sign?

Format for Lookup Table Files

As described above, a user can define a lookup key, such as:

Section = “W8x18”

then ClariCalc will populate variables with values from a lookup table, based on the lookup key.

This section tells you how to write your own lookup table. To begin, all lookup table files must be located in subdirectory C:\Users\userID\AppData\Roaming\Hilbert\. There can be more than one such file.

In that folder, ClariCalc will examine all the files named: LookupTable*.txt. If you have ClariCalc Pro, you may already have two such files—LookupTableStructural.txt and LookupTableElectrical.txt.

LookupTable files must be written in a particular format. The next few lines show an example:

Categories:	Section	Steel
W	wself	A	d	tw	bf	tf
Section	plf	in²	in	in	in	in
W8x31	31	9.12	8	8	0.285	0.435
W8x28	28	8.24	8.06	6.54	0.285	0.465
W8x24	24	7.08	7.93	6.5	0.245	0.4
W8x21	21	6.16	8.28	5.27	0.25	0.4
W8x18	18	5.26	8.14	5.25	0.23	0.33
Steel Grade	Fy	Fu	Ry	Rt
Steel	ksi	ksi
ASTM A36	36	58
ASTM A36 plates	36	58	1.3	1.2
ASTM A992	50	65	1.1	1.1

The file’s first line has tab-delimited values that define the categories of the possible lookup keys. This example has two categories, so the user would be able to define such lookup keys as:

The file’s second line must be blank.

The remainder of the file is a series of tab-delimited data sections. The top row of each section contains the variable names that the document will inherit after a lookup key is defined. The second row of each section defines the unit of measure for each variable.

The rest of the rows in each section contain the data. First comes the lookup key, then a value for each variable.

Now let me modify what I said about the first two rows of each section. The first word in each of those rows is used to help the operation of the dialog box that allows a user to choose a Lookup Key from a list.

The first row’s first word will populate the Group list on the left hand side of the dialog box.

The second row’s first word will define the category of the lookup key, such as Section or Steel.

Each section must be separated from other sections by a blank line.

Save the text file in UTF-8 text format.

When a user wants to access this data, they will do it in two steps.

1. Define the lookup key, e.g., Section = “W8x24”
2. Call a variable in a calculation, e.g., d = 7.93 in.

ClariCalc Precision

Internally, ClariCalc holds numbers in memory using either a Decimal data type or a Double (64 bit floating) data type. The Decimal numbers have precision of 28 digits or less. Doubles have approximately 15 digit precision.

Precision limits like these can create problems that you might not expect. Problems when you test for equality, problems in subtraction, problems with overflow. John Cook explains them well here.

During a recalculation, ClariCalc internally holds the result of each operation with maximum precision. These internal values are discarded when the recalculation ends. For subsequent recalculations, ClariCalc uses the value displayed on the page or screen, which may have been rounded to a less precise value when it was written into the document.

Specialties

ClariCalc goes beyond the calculation engine in ClariCalc and provides several additional capabilities. These are described in other pages of this website:

• Beam Analysis
• Structural
• Projects
• Electrical

Updates

ClariCalc updates are free. To get the latest version of basic ClariCalc, use the Download button in the left sidebar. ClariCalc was last modified on 28 March 2018.

Copyright © 2016 - 2019 Hilbert LLC

Contents

• Introduction
• The Basics
• Writing Math
• Syntax▼
  • General
  • ClariCalc Notation
  • Operators
  • Functions
  • Constants
  • Operator Precedence
  • If Expressions
  • Rounding
• Variables▼
  • General
  • Assignments
  • Bookmarks
  • ParentFiles
  • Lookup Table
  • Tables
  • Dictionaries
• Units▼
  • … in calculations
  • … in variables
  • Weight
  • Traditional Units
  • Currency Rates
• Re-Calculation
• Beyond Reals▼
  • General
  • Dates
  • Arrays
  • Comprehensions
  • Matrices
  • Vectors
  • Complex Numbers
• Shortcuts▼
  • Keyboard Shortcuts
  • Quick Parts
• Extra▼
  • Tables
  • Sum a Column
  • Ok / ng
• Appendices▼
  • Troubleshooting
  • Lookup Table Format
  • ClariCalc Precision
• Specialties▼
  • General
  • Beam Analysis
  • Structural
  • Projects
  • Electrical
  • Updates

Download ClariCalc